Q2

Q1

Question 3

Q1.

T1W4 Quiz 3

Quadratic Equations and Inequalities (Part 1)

The Gateway Arch is a 630-foot (192 m) high monument in St. Louis, in the U.S. state of Missouri. Built as a monument to the westward expansion of the United States, it is the centerpiece of the Jefferson National Expansion Memorial and has become an internationally famous symbol of St. Louis. 

(http://en.wikipedia.org/wiki/Gateway_Arch)

Essential Questions

1     What makes a parabolic curve so aesthetically pleasing as an architectural structure?

2    Do you think the above structure represents a parabolic curve?

What is a Function?

A function relates an input to an output.

It is like a machine that has an input and an output. And the output is related somehow to the input.

f(x)	"f(x) = ... " is the classic way of writing a function. And there are other ways, as you will see!

First, it is useful to give a function a name. The most common name is "f", but you can have other names like "g" ... or even "marmalade" if you want. But let's use "f": You would say "f of x equals x squared" what goes into the function is put inside parentheses () after the name of the function: So f(x) shows you the function is called "f", and "x" goes in And you will often see what a function does with the input: f(x) = x2 shows you that function "f" takes "x" and squares it. Example: with f(x) = x2: an input of 4 becomes an output of 16. In fact we can write f(4) = 16.  Example: this tree grows 20 cm every year, so the height of the tree is related to its age using the function h: h(age) = age × 20 So, if the age is 10 years, the height is: h(10) = 10 × 20 = 200 cm Here are some example values: age h(age) = age × 20 0 0 1 20 3.2 64 15 300 ... ... 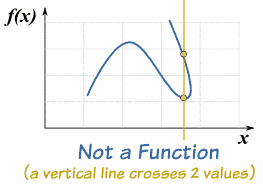A Function is Special But a function has special rules: It must work for every possible input value And you can only have one relationship for each input value This can be said in one definition: Formal Definition of a Function A function relates each element of a set with exactly one element of another set (possibly the same set). The Two Important Things! 1. "...each element..." means that every element in X is related to some element in Y. We say that the function covers X (relates every element of it). (But some elements of Y might not be related to at all, which is fine.) 2. "...exactly one..." means that a function is single valued. It will not give back 2 or more results for the same input. So "f(2) = 7 or 9" is not right!   (one-to-many)   (many-to-one) This is NOT OK in a function   But this is OK in a function If a relationship does not follow those two rules then it is not a function ... it would still be a relationship, just not a function. 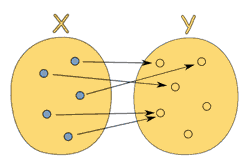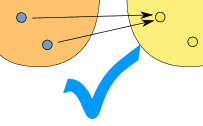Example: The relationship x → x2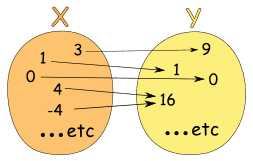 Could also be written as a table: X: x Y: x2 3 9 1 1 0 0 4 16 -4 16 ... ... It is a function, because: Every element in X is related to Y No element in X has two or more relationships So it follows the rules. 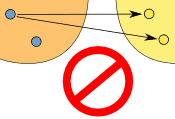(Notice how both 4 and -4 relate to 16, which is allowed.) Example: This relationship is not a function: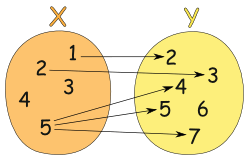 It is a relationship, but it is not a function, for these reasons: Value "3" in X has no relation in Y Value "4" in X has no relation in Y Value "5" is related to more than one value in Y (But the fact that "6" in Y is not related to does not matter) Vertical Line Test On a graph, the idea of single valued means that no vertical line would ever cross more than one value. If it crosses more than once it is still a valid curve, but it would not be a function.

Ordered Pairs

I said I would show you many ways to think about functions, and here is another way:

You can write the input and output of a function as an "ordered pair", such as (4,16).

They are called ordered pairs because the input always comes first, and the output second:

(input, output)

So it looks like this:

( x, f(x) )

Example:

(4,16) means that the function takes in "4" and gives out "16"

Set of Ordered Pairs

A function can then be defined as a set of ordered pairs:

Example: {(2,4), (3,5), (7,3)} is a function that says

"2 is related to 4", "3 is related to 5" and "7 is related 3".

Also, notice that:

• the domain is {2,3,7} (the input values)
• and the range is {4,5,3} (the output values)

Conclusion

• a function relates inputs to outputs
• a function takes elements from a set (the domain) and relates them to elements in a set (the codomain).
• all the outputs (the actual values related to) are together called the range
• a function is a special type of relation where:
  • every element in the domain is included, and
  • any input produces only one output (not this or that)
• an input and its matching output are together called an ordered pair
• so a function can also be seen as a set of ordered pairs

The Vending Machine analogy

A function has input and output. A good analogy of this would

be a vending machine.

1. Explain further why this analogy is used to depict a function?
2. Can you think of other analogy?
3. What are the assumptions made?

Function and relation

1. If you say 2, I'll say 11. If you say 7, I'll say 26. Can you determine why I say what I say?

2. If you say 2, I'll say (-3). If you say 7, I'll say 7. Can you determine why I say what I say?

3. If you say 2, I'll say 3. If you say 7, I''ll say 21. Can you determine why I say what I say?

Materials

1. Maths notes (given by school)

2. Maths Exercise book (for note taking and class discussion)

3. Calculator

4. Writing materials (Pens & Pencils) + Ruler

5. Learning Device

Others:

1. Textbook is optional

2. Maths file (orange)

3. Remedial (Every Monday 3 pm to 4 pm)