What is a Function?
A function relates an input to an output.
 |
It is like a machine that has an input and an output.
And the output is related somehow to the input.
|
| f(x) |
"f(x) = ... " is the classic way of writing a function.
And there are other ways, as you will see!
|
|
First, it is useful to give a function a name.
The most common name is "f", but you can have other names like "g" ... or even "marmalade" if you want.
But let's use "f":
You would say "f of x equals x squared"
what goes into the function is put inside parentheses () after the name of the function:
So f(x) shows you the function is called "f", and "x" goes in
And you will often see what a function does with the input:
f(x) = x2 shows you that function "f" takes "x" and squares it.
Example: with f(x) = x2:
- an input of 4
- becomes an output of 16.
In fact we can write f(4) = 16.
Example: this tree grows 20 cm every year, so the height of the tree is related to its age using the function h:
h(age) = age × 20
So, if the age is 10 years, the height is:
h(10) = 10 × 20 = 200 cm
Here are some example values:
| age | h(age) = age × 20 |
|---|
| 0 | 0 |
| 1 | 20 |
| 3.2 | 64 |
| 15 | 300 |
| ... | ... |
A Function is Special
But a function has special rules:
- It must work for every possible input value
- And you can only have one relationship for each input value
This can be said in one definition:
 |
Formal Definition of a Function
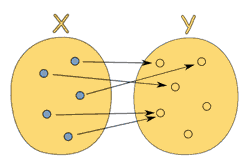
A function relates each element of a set
with exactly one element of another set
(possibly the same set).
|
The Two Important Things!
1.
|
"...each element..." means that every element in X is related to some element in Y.
We say that the function covers X (relates every element of it).
(But some elements of Y might not be related to at all, which is fine.)
|
2.
|
"...exactly one..." means that a function is single valued. It will not give back 2 or more results for the same input.
So "f(2) = 7 or 9" is not right!
|
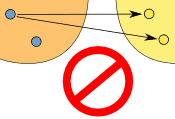 | | 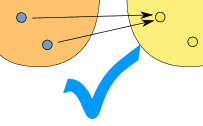 |
| (one-to-many) | | (many-to-one) |
| This is NOT OK in a function | | But this is OK in a function |
If a relationship does not follow those two rules then it is not a function ... it would still be a relationship, just not a function.
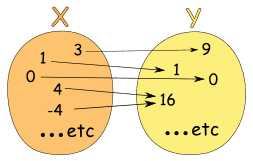
Example: The relationship x → x2
Could also be written as a table:
| X: x | Y: x2 |
|---|
| 3 | 9 |
| 1 | 1 |
| 0 | 0 |
| 4 | 16 |
| -4 | 16 |
| ... | ... |
It is a function, because:
- Every element in X is related to Y
- No element in X has two or more relationships
So it follows the rules.
(Notice how both 4 and -4 relate to 16, which is allowed.)
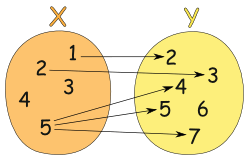
Example: This relationship is not a function:
It is a relationship, but it is not a function, for these reasons:
- Value "3" in X has no relation in Y
- Value "4" in X has no relation in Y
- Value "5" is related to more than one value in Y
(But the fact that "6" in Y is not related to does not matter)
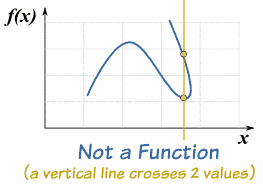 |
Vertical Line Test
On a graph, the idea of single valued means that no vertical line would ever cross more than one value.
If it crosses more than once it is still a valid curve, but it would not be a function.
|
|
Ordered Pairs
I said I would show you many ways to think about functions, and here is another way:
You can write the input and output of a function as an "ordered pair", such as (4,16).
They are called ordered pairs because the input always comes first, and the output second:
(input, output)
So it looks like this:
( x, f(x) )
Example:
(4,16) means that the function takes in "4" and gives out "16"
Set of Ordered Pairs
A function can then be defined as a set of ordered pairs:
Example: {(2,4), (3,5), (7,3)} is a function that says
"2 is related to 4", "3 is related to 5" and "7 is related 3".
Also, notice that:
- the domain is {2,3,7} (the input values)
- and the range is {4,5,3} (the output values)
Conclusion
- a function relates inputs to outputs
- a function takes elements from a set (the domain) and relates them to elements in a set (the codomain).
- all the outputs (the actual values related to) are together called the range
- a function is a special type of relation where:
- every element in the domain is included, and
- any input produces only one output (not this or that)
- an input and its matching output are together called an ordered pair
- so a function can also be seen as a set of ordered pairs